サンプル parametric_lsys.gh

Figure 1.36　Figure 1.37 a で紹介されているパラメトリック L-Systemのコードの書き方です。文字 ‘F’ によって前方に向かって線を書く際に、その長さにパラメータを持たせ長さを（周期的に）変化させる、というものです。簡潔でロバスト（応用性が高くフレキシブル）なこれまでの書き方を模索していましたが、やむを得ずすこしコンポーネントと構造を改修することにしました。

基本的な考え方は、’F’のパラメータを別途数字のリストとして用意し、

これまで文字列のみで表現していた s = ‘F+F+F–‘ を　文字と数値のリストを組み合わせたリスト、にします。
[‘F+-FF’,[0.5,1.0,0.3]]
[文字,[数,数,数,数,数]] という入れ子にします。

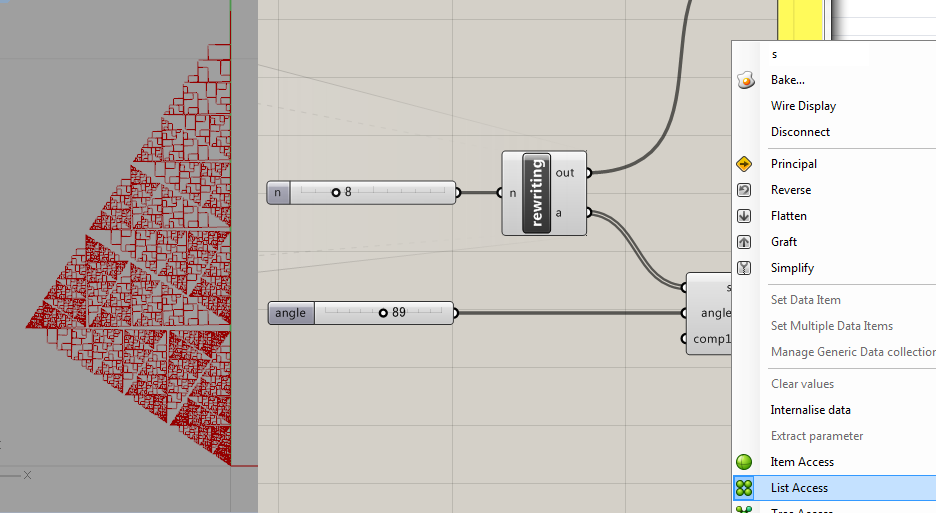
コンポーネント”rewrite”から　a = s としてl-Systemのパターンを出力するき、文字だけでなく上記の入れ子のリストを送ります。コンポーネント generate 側の s の入力をリストアクセスListAccessに変更するのを忘れずに。

generate側では、 s_p として、文字列パターンと、パラメータリストを受け取り

    ptn = s_p[0]
    prm = s_p[1]

    prmCount = 0

として、文字列とパラメータリストを分離します。 prmCount という整数を用意して、’F’（など） が描画されるたびにprmのリストの位置をずらしていきます。
prm の中のパラメータを適用させながら描画を進めます。generateコンポーネントの中の”generate(ptn):” 関数の中で使われるvの変化のさせ方も変更します。ベクトル v を長さ 1.0 にリサイズして、prmのパラメータで大きさをリサイズします。

        elif ptn[i] == 'F':
            #here we generate Rhino object
            if(len(prm)):
                v = rs.VectorUnitize(v)
                v *= prm[prmCount]

            line = rs.AddLine(p,p+v)
            objs.append(line)          

            if comp1 != None:
                tfr = rg.Transform.Rotation(rg.Vector3d(0,0,1),v,p)
                tfm = rg.Transform.Translation(p[0],p[1],p[2])
                tf = rg.Transform.Multiply(tfr,tfm)
                ob = rs.CopyObject(part1)
                rs.TransformObject(ob,tf)
                objs.append(ob)

            p = p + v
            prmCount += 1

Figure 1.36で説明されているパラメータですが、以下のように c, p で一意に決まる、p,q,h が使われます。これらの数値で三角形の形を決めています。

c = 1
p = 0.3
q = c - p
h = math.sqrt(p*q)

初期値や書き換えルールは以下のように記述します。

s_p = ['F',[1]]
for i in range(1,int(n)):
    s_p = rewriteSP(s_p,'F','F+F--F+F',[p,h,h,q])

‘F+F–F+F’　と　[p,h,h,q]　の部分、要素の数（’F’の数と[]の中の要素数、この場合４）を、等しくすることが要件です。
これが唯一の方法ではありませんが、いかがでしょうか。